Unterrichtsmaterial
Unterrichtseinheiten
- Download: Unterrichtseinheiten zum Fachrechnen
Rechnen mit Einheiten
Wer Bremspedal und Kupplung nicht ohne zu überlegen bedienen kann, wird nie ein guter Autofahrer, und wessen Gehirn schon mit dem Umformen von Gleichungen und dem Rechnen mit Einheiten ausgelastet ist, wird den Kopf nicht frei haben, um das technische Problem zu verstehen.
Um dies etwas üben zu können, habe ich die falsch gelösten Aufgaben einiger Klassenarbeiten zusammengestellt: Übungsaufgaben zum Rechnen mit Einheiten.
Kopfrechnen mit "Zuletzt gewinnt"
"Zuletzt gewinnt" ist ein Lernspiel, mit dem Kopfrechnen geübt werden kann.
Spielgedanke: Zwei Spieler spielen auf einem Spielfeld mit Zahlen von 1 bis z.B. 100. Im ersten Zug streicht ein Spieler eine beliebige Zahl. In den weiteren Zügen streichen die Spieler abwechselnd je eine Zahl, die ein Teiler oder ein Vielfaches der Vorhergehenden sein muss. Verloren hat, wer keine erlaubte Zahl mehr findet. Wenn ein Spieler gewinnen will, muss er Züge vorausberechnen und übt so das Kopfrechnen.
Es spielen zwar nur 2 Spieler mit- bzw. gegeneinander, aber wenn man kurze Zahlenreihen verwendet, sind auch kleine Turniere für Gruppen möglich.
Herstellung des Spieles
- Am einfachsten ist das Spiel im Unterricht durchzuführen, wenn man Regeln, ein Beispiel und das Spielfeld auf ein DIN-A4-Blatt druckt und laminiert. Man kann so leicht mehrere Spielfelder herstellen und im Ordner aufbewahren. Gespielt wird mit wasserlöslichen Stiften, die nach dem Spiel einfach abgewischt werden können. Hier können Sie das Spiel mit Regeln, Beispiel und Spielfeld 1 bis 100 bzw. mit Regeln, Beispiel und Spielfeld 1 bis 225 herunterladen (PDF, je 13kB).
- In einer aufwändigeren Fassung spielt man mit Karten. Dazu finden Sie hier die Regeln mit Beispiel (PDF, 13kB) und ein Tabellenkalkulationsblatt zum Ausdruck von Zahlen-Karten (XLS, 90KB, für Excel, LibreOffice / OpenOffice oder StarOffice).
Kostenrechnungen
Der Kostenvergleich zwischen Fahrzeugen mit Otto- und Dieselmotoren siehe Lernfeld 01 für Kfz-Mechatroniker .
Statik
- Drehmoment ist Kraft mal Hebelarm (PDF, 43kB): Unterrichtsplanung zur Vorbereitung von Auflagern.
Drehmoment - Leistung - Drehzahl - Übersetzungen - Geschwindigkeit
Siehe Lernfeld 01 für Kfz-Mechatroniker .
Winkelfunktionen
- Download: Einführung in Winkelfunktionen (PDF): Arbeitsblatt mit Lösungen.
- Download: Regeln in rechtwinkligen Dreiecken (PDF): Arbeitsblatt mit Lösungen.
- Download: Übungen zu rechtwinkligen Dreiecken (PDF): Arbeitsblatt mit Lösungen.
- Download: Verlauf der Winkelfunktionen ermitteln (PDF): Arbeitsblatt mit Lösungen.
- Download: Kontrollmaßberechnung (PDF): Übungen zu Kontrollmaßen (Schwalbenschwanz, Führung, Prisma, Keilriemenscheibe) als praktische Anwendung von rechtwinkligen Dreiecken.
- Download: Übungen zum Berechnen vom CNC-Koordinaten
- Link: Einführungskurs in Trigonometrie von Daniel Brugger (Absolvent des TG Lörrach, 04/2003)
- Download: Pyramidalabweichung (PDF): Berechnungsbeispiel und Anwendungsfälle der Pyramidalabweichung.
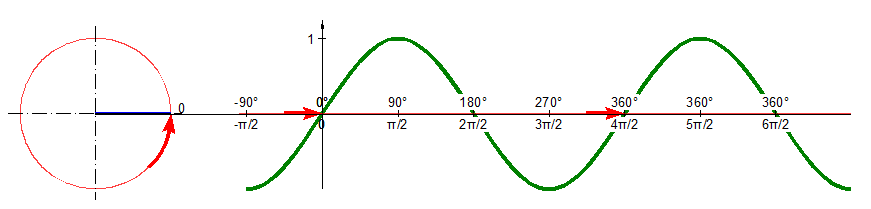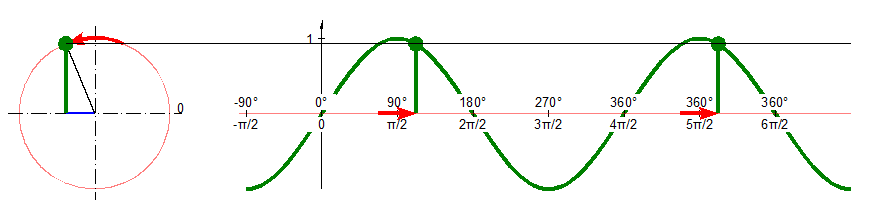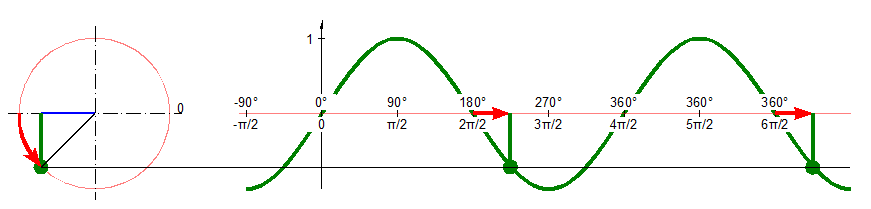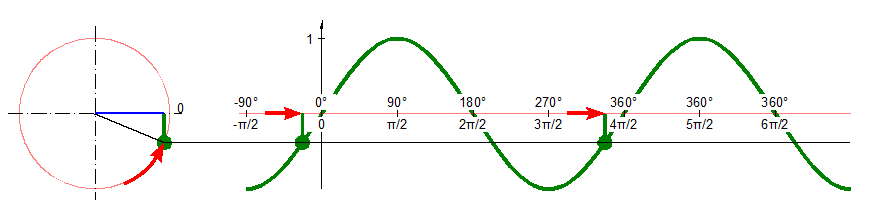
Einheitskreis und Sinusfunktion
Die Rettung: CAD statt Winkelfunktionen
Wenn man Winkelfunktionen nur benötigt, um konkrete Längen zu ermitteln, gib es eine pragmatische Lösung ohne Mathematik: Man zeichnet das Problem in CAD und misst die gesuchte Länge in beliebiger Genauigkeit ab.
Beispiel
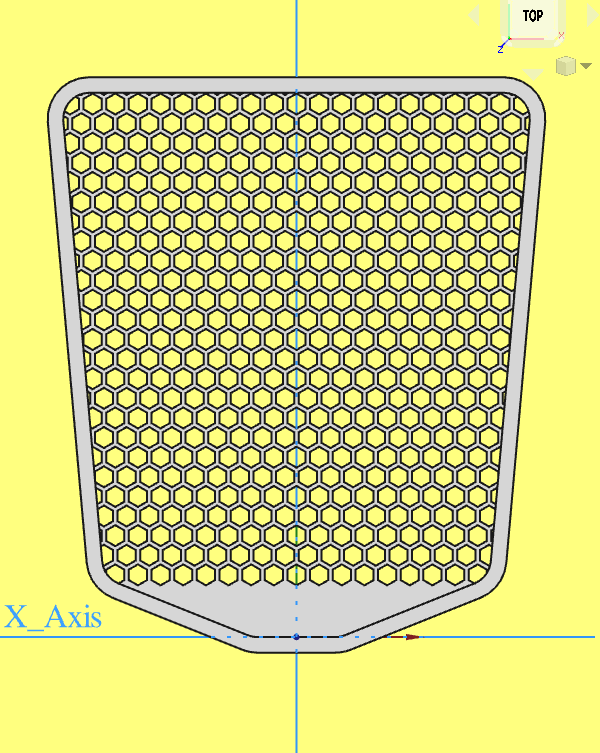
Abb. Fliegenklatschenblatt
Das Beispiel stammt aus dem Tutorial Fliegenklatsche mit FreeCAD.
Das Wabenmuster im Fliegenklatschenblatt besteht aus regelmäßigen Sechsecken SW3,5 (SW = Schlüsselweite [mm] = Inkreisdurchmesser). Die Wandstärke zwischen den Sechsecken beträgt 0,87 mm.
Wie groß sind die Abstände (Mitte - Mitte) zwischen …
- … zwei waagerecht benachbarten Sechsecken (ax)?
- … zwei schräg benachbarten Sechsecken (as)?
- … zwei genau senkrecht übereinander stehenden Sechsecken der ersten und der dritten waagerechten Reihe (ay)?
Lösung
Für waagerecht und schräge Nachbarn setzt sich die Lösung zusammen aus der Schlüsselweite des Sechskants und der Wandstärke, also:
ax = as = 3,5 mm + 0,87 mm = 4,37 mm.
Für den senkrechten Abstand zwischen zwei Mustern könnte man Winkelfunktionen bemühen:
ay = 2 * (Schlüsselweite + Wandstärke) * cos 30°
ay = 2 * 4,37 mm * 0,866 = 7,569 mm.
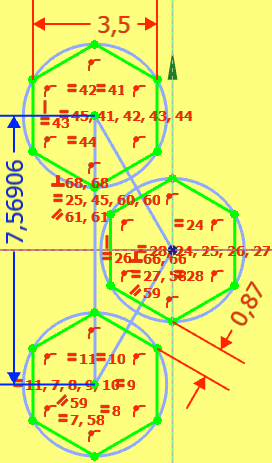
Abb. Lochabstand ay
Oder man skizziert einen Ausschnitt des Musters mit FreeCAD (oder einem anderen CAD-Programm) und misst den senkrechten Abstand (siehe Abb. Lochabstand).
Man erkennt drei identische Sechsecke mit SW3,5, Wandstärke 0,87 und der gewünschten Anordnung. Die Maße sind nur je einmal eingetragen und dann durch die Funktion gleiche Länge übertragen.
Die Skizze ist hellgrün, also vollständig bestimmt. Das letzte Maß 7,569 ist blau dargestellt und das bedeutet, dass dieses Maß eigentlich nicht mehr nötig ist, weil es durch die anderen Maße bestimmt ist.
Im Maschinenbau nennt man solche Maße Hilfsmaße und stellt sie in Klammern dar. In FreeCAD muss man für solche Maße beim Bemaßen Referenz einschalten, damit man keine Fehlermeldung bekommt.
Hinweise:
- Auf Taschenrechnern hat sich die Schreibweise \(sin^{-1}, cos^{-1}\) und \(tan^{-1} \) statt arcsin, arccos und arctan eingebürgert. Diese Schreibweise darf in Formeln nicht verwendet werden, da sie dort mit \(tan^{-1} = \frac {1}{tan} = cot \) verwechselt werden kann.
- Der Cotangens erscheint auf Taschenrechnern meist gar nicht mehr, vermutlich um eine Taste zu sparen. Der Cotangens kann aber durch Zusammenhang \(cot = \frac {1}{tan} \) leicht ersetzt werden
- In Tabellenkalkulationen haben sich die korrekten Schreibweisen erhalten.
- Beim Schreiben von Formeln verwende ich immer die Reihenfolge \(x = y \cdot sin \alpha \) statt \(x = sin \alpha \cdot y \), weil dadurch die Verwechslungsgefahr etwas geringer ist. So etwas kostet nichts außer ein bisschen Sorgfalt, kann aber in Klassenarbeiten ganze Noten ausmachen.
- Das Wort 'Sinus' kommt aus dem Lateinischen und bedeutet dort 'Bogen'. Den Grund für diese Wortwahl findet man im Verlauf der Sinuskurve (siehe oben).
Sonstiges
- Link: Dennis Rudolph bemüht sich, im Bereich Mathematik der Seite Frustfrei-Lernen.de, Mathe-Stoff auf möglichst einfache Art und Weise zu erklären. (07/2009)
- Link: Wolfram Alpha ist ein neuer Ansatz, Wissen im Netz zu finden. (05/2009) Beim Rechnen hilft es. Versuchen Sie: integrate x^3 sin^2 x dx
- Link: Mathematik und Physik für Schüler, Lehrer und Eltern von Rudolf Brinkmann erklärt den Stoff bis zum Abi. (09/2008)
- Link: Mathe-Seiten von Peter Otto mit Übungen und Erklärungen zum Hauptschulstoff, vor allem Prozentrechnung. (09/2008)
- Link: eMath mit Material zur Vorbereitung des Mathe-Abiturs. (03/2002)

